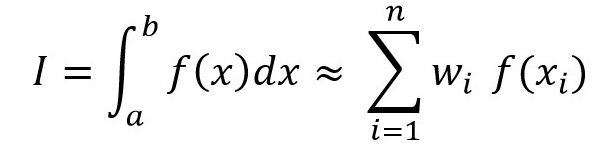
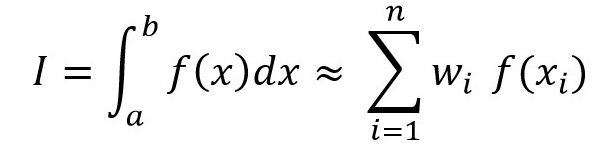
For a function of two variables it is equivalent to finding an approximation to the volume under the surface. Numerical integration is often also referred to as quadrature or sometimes cubature for functions of two or more variables. Returning to the one variable case, numerical integration involves finding the approximation to an integral of a function f(x) through its evaluation at a set of discrete points. There are two distinct approaches to this. Firstly methods like the trapezium rule or Simpson's rule determine the integral through evaluating f(x) at regularly spaced points. These are generally referred to as Newton-Cotes formulae.
Alternative methods termed Gaussian Quadrature methods have arisen that select irregularly-placed evaluation points, chosen to determine the integral as accurately as possible with a given set of points.
Gaussian Quadrature methods are important as they often lead to very efficient methods. In numerical integration the efficiency of the method relates to the accuracy obtained with respect to the number of evaluations of the function f(x). In intensive methods such as the boundary element method integrations may need to be performed millions of times so the efficiency of the methods needs to be considered sometimes.
In general, care must be taken to match the numerical integration method to the expected nature of the function f(x). Typically, it may be known that f(x) is regular. On the other hand f(x) may be singular or oscillatory and will then need special treatment. Often a special method called a product integration method can be developed for the integration of functions of the form f(x) = w(x)g(x) where w(x) is a pre-set function and the function and g(x) is known to be a relatively nice function.
For an introduction to numerical integration methods please see Numerical Integration or Quadrature .
Mid-point Integration Rule : Excel Spreadsheet Demo
Trapezoidal Integration Rule : Excel Spreadsheet Demo
Simpson's Integration Rule : Excel Spreadsheet Demo
Gaussian Quadrature (Gauss-Legendre) : Excel Spreadsheet Demo